2025. 12. 25. 20:39ㆍElectronic Engineering/전자기학(전기기사)
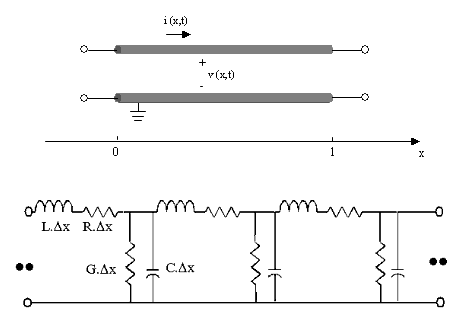
자고로 송전선은 선처럼 보이지만, 사실 물리적으로는 "아아아아아아주주주주주길게 늘어진 회로 덩어리"라서 분포정수회로로 간주해야만 한다. 여기서 분포 정수 회로란, R/L/C가 고르게 퍼져 있음을 말하며 반대로 R/L/C가 덩어리처럼 뭉쳐 있을 경우를 덩어리 회로라고 한다.
쨋든 이게 문제는 아니고, 저 빌어먹을 분포정수회로를 어떻게 해석하느냐가 문제인데. 이는 사고실험을 통해서 적당히 해석할 수 있다. 대충 송전선을 아주 짧은 길이 deltaX만큼 잘라서 보면...

이 작은 조각 하나가 나오게 된다. 그리고 여기에는 항상 네가지가 따라 붇는다. 이중 Rx는 도선 자체의 저항이고, Lx는 전류가 흐르며 생기는 자기장, Cx는 두 도선 사이의 전기정, Gx는 절연체 누설로 해석할 수 있다. 그리고 이걸 엄청 많이 직렬/병렬로 이어 붙인게 실제 송전선이 된다. 참고로 보통 R, L, C, G는 길이 1m단위로 치고, 송전선에서의 G는 '절연누설'을 따로 나타내는 항이다. 일반 회로의 컨덕턴스 마냥 생각하면 살짝 머리가 복잡해 질 수 있다.
그래서, 결론적으로 송전선의 선로 정수는 아래와 같이 적을 수 있다.
이때 특성 임피던스라는 기기괴괴한게 나타나는데, 대충 "송전선이 무한히 길다고 가정했을 때 그 선이 보여주는 전압/전류의 비"다. 반사파/투과파가 없다 치고 송전선에 신호를 딱 넣었을 때 V/I의 값인 셈이다. 참고로 부하가 없다 쳐도 왜 임피던스가 나오는 지 의아할 수 있는데, 현실에서 전류가 흐른다는건 에너지가 일부는 손상된다는 것을 의미하기 때문이다.
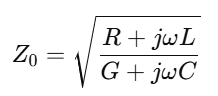
이때 송전 손실이 없다고 치거나(R=G=0) 무왜형일 경우(RC=LG)일 때에는 특성 임피던스가 root(L/C)에 다다르게 된다. 물론 이런 경우는 현실에서 찾아보기 극악스럽게 어렵겠지만.. 뭐 어쨋든 시험 문제를 풀어야 하긴 하므로. 참고를 해야 한다.
그리고 우리 위대한 수학은, 파동이 어떻게 이동되면서 변형되는지를 복소수 상수로 표현해 줄 수 있게 하니. 이것을 바로 전파정수라고 하게 되며, 식은 아래와 같다.
이때 알파를 감쇠정수(V/m), 베타를 위상정수(rad/m)라고 하게 된다. 감쇠정수는 무한장 선로에서 단위길이당 전압의 크기가 감쇠하는 비율을, 위상 정수는 무한장 선로에서 단위길이당 전압의 위상이 감쇠하는 비율을 말하게 된다. 참고로 무왜형/무손실에서 베타의 값은 w*root(LC)의 값으로 동일하나, 무왜형에서 알파의 값이 sqrt(RG)/무손실에서 알파=0인 것이 차이다.
덤으로, 베타의 경우 위상정수가 되는데... 아래 공식에 따라 전파 속도/파장을 구할 수 있게 된다.
'Electronic Engineering > 전자기학(전기기사)' 카테고리의 다른 글
| 3상 동기 발전기의 구조/이론(1) (0) | 2026.01.13 |
|---|---|
| T형 회로와 파이형 회로의 4단자 정수 (0) | 2025.12.18 |
| 4단자망의 기본식 (0) | 2025.12.17 |
| 비정현파 AC (0) | 2025.12.16 |
| RLC회로와 벡터 (0) | 2025.12.12 |





