2025. 11. 30. 20:09ㆍElectronic Engineering/전자기학(전기기사)
대충 전기 퍼텐셜 같?은 스칼라 장이 있다고 치자. 이때 라플라시안을 갈긴 것이 상수이고, 0이 아니라면

과 같은 식을 만족하게 된다. 이를 전기 퍼텐셜에서의 포아송 방정식이라고 생각할 수 있다. 근데 이게 처음 보면 도대체 뭔소리인지 감이 잘 안잡힐텐데 - 일단 Field에 대한 포아송 방정식에 대해서 이해를 하고 좀 넘어가자.
자고로 벡터 미적분학에서 지겹게 보는 기호는 나블라(델) 기호인데, 간혹 가다가 이게 무슨 스퀘어처럼 되어 있는 마냥 되어있는 경우가 있다. 이를 라플라시안(Laplacian)이라고 하며, 대충 Gradient 한거에 Divergence를 박은 것이다.
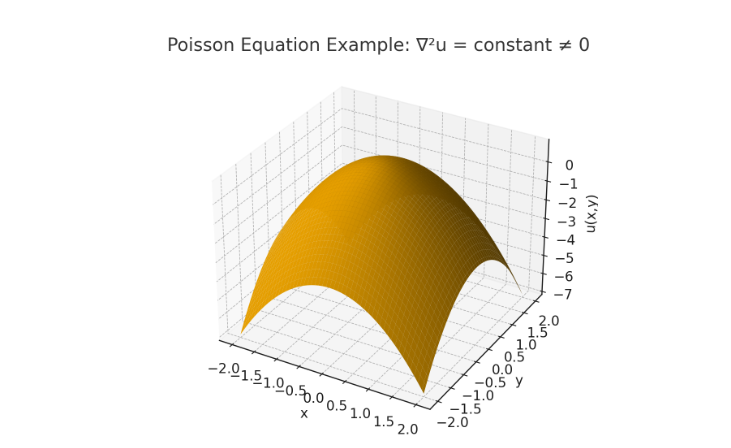
근데 이게 무슨 의미가 있느냐 하면은, 마치 이계도 함수마냥 어떤 장의 곡률을 측정할 수 있게 된다. 대충 위의 그래프를 생각해보면 - 저기에 Gradient를 박으면 안쪽으로 몰린 벡터가 나올 것이다. 그리고 이걸 Divergence 연산 하면 (-)인 스칼라 값이 나올 것이다. 축하한다, 방금 당신은 공간이 얼마나 휘는지(곡률)을 측정해 냈다.

그리고 위에서의 사실을 전기 퍼텐셜에 가져다 쓰면 위의 수식이 말하고자 하는 바가 나온다. 즉슨, 전기 퍼텐셜이 얼마나 휘는지(전위의 곡률)은 그 안에 얼마나 전하가 들어있는 지에 대해서 좌우된다는 것이다. 참고로 이는 가우스 법칙의 미분형에, 전계를 전위의 Gradient로 치환해서 때려 박으면 나온다. (Divergence(전계밀도) = 전하밀도)
그리고 여기서 등장하는 또다른 단어가 라플라스 방정식인데, 쉽게 말해서 얘는 라플라시안 때렸을때 0이 나오는 상황을 말하는 것이라고 보면 된다. 그리고 이것이 의미하는 바는 - 전기 퍼텐셜의 곡률이 없으므로 "전하가 없는 상황"과 동일하다.
이게 이해가 잘 안될수도 있는데 - 예를 하나 들어보자. 길게 펼친 고무 막에 볼링 공을 던져본다 치면, 곧 공이 떨어진 자리 밑으로 고무막이 움푹 들어갈 것이다. 그리고 움푹 들어간 만큼은 - 퍼텐셜이라고 이해 할 수 있을 것이다. 근데 공이 없다면? 그냥 일정 부분은 평-평하게 곡률이 없을 것이고.. 그러면 거기에는 그냥 아무것도 없는 셈이 될것이다. 이걸 전기 퍼텐셜로 치환하면 - 라플라스 방정식이 이해가 될 것이다.

'Electronic Engineering > 전자기학(전기기사)' 카테고리의 다른 글
| RLC회로와 벡터 (0) | 2025.12.12 |
|---|---|
| 히스테리시스 곡선 (0) | 2025.12.08 |
| 비오-사바르 법칙과 자계 (0) | 2025.12.05 |
| 전기 영상(Projection)법 (0) | 2025.12.03 |
| 전기장에서의 가우스 법칙 (0) | 2025.12.01 |
