2025. 12. 18. 15:38ㆍComputer Science/AI(ML, DL, RL, etc)

AI를 설계하기 위해서 생물학적 모티브를 따와, 맥컬록과 피츠는 간소화된 뉴런의 개념을 발표했다. 이를 맥컬록-피츠 뉴런(MCP)이라고 하며, 추후 얘기하게 될 퍼셉트론이라는 개념의 모티브가 된다. 쨋든 이양반들은 뉴런을 아주 단순하게 생각해서 아래와 같은 간단한 무엇인가를 내놓게 된다.
신경세포는 Na+ K+채널을 써서 재분극이니 탈분극이니 하는 복잡한 과정이 필요한데, 다 던지고 이진 출력을 내는 간단한 논리회로로 표현해 보자.
그리고 이게 발전된게 로젠블라트의 퍼셉트론이다. 이걸 좀 형식적으로 얘기하자면, 이전 신경세포에서의 가중치를 w라 치고 입력을 x라 치면 현재 신경세포에서의 출력은
가 될 것이다. 물론 현행 신경 세포도 역치값을 넘겨야지 신호를 전달하게 끔 해야 하므로, 아래와 같은 결정함수를 생각하게 된다. 사실 이건 이진 분류 기준이고, 나중에 가면은 별의 별 함수가 다 나오게 된다.
그리고 퍼셉트론의 학습 규칙은 아래를 따르게 된다.
- 가중치를 0 또는 랜덤한 작은 값으로 초기화 한다.
- 각 훈련 샘플에서 출력값을 계산하고, 가중치와 절편을 업데이트 한다.
이때 뜬금없이 eta가 들어가 있는데, 얘는 학습률을 의미하게 된다. 앞에 델타가 붙은 것은 업데이트 값이 되고, hat이 붙어 있는 얘는 예측값이다. 그리고 퍼셉트론은 두 클래스가 선형적으로 구분될 때에만 수렴이 보장된다. 만약 그렇지 않다면 훈련을 반복할 최대 횟수(epoch)를 정해야만 한다.
import numpy as np
class Perceptron:
def __init__(self, eta = 0.01, n_inter = 50, random_state = 0):
self.eta = eta
self.n_inter = n_inter
self.random_state = random_state
def fit(self, X, y):
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0, scale=0.01, size=X.shape[1])
self.b_ = np.float64(0.)
self.errors_ = []
for _ in range(self.n_inter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi))
self.w_ += update * xi
self.b_ += update
errors += int(update != 0.0)
self.errors_.append(errors)
def net_input(self, X):
return np.dot(X, self.w_) + self.b_
def predict(self, X):
return np.where(self.net_input(X) >= 0.0, 1, 0)코드로 구현하면 대걍 이렇게 된다. 아 물론 가중치를 0으로도 둘 수 있겠다만, eta 파라미터가 영향을 못 미치기에 영 찝찝한 관계로 rgen으로 가중치를 생성 해주고 지지고 볶는다.
이제 이 퍼셉트론을 가져다가 붓꽃 데이터에다가 한번 써보자.

대충 붓꽃 데이터는 이렇게 생겨 먹었다. 어째 선형적으로 구분하기 딱 좋게 생겨 먹었음으로, 위에서 만들어 둔 퍼셉트론에 이 데이터를 박아다가 학습 시켜보자.

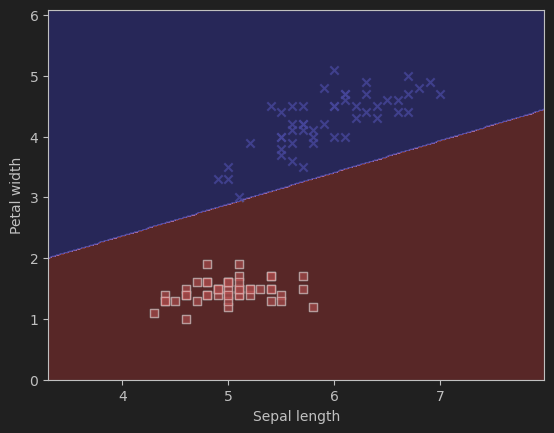
Epochs가 7정도 된 순간 오차가 거의 0에 근접함을 볼 수 있다. 이제 적당한 분류기로 써먹을 수 있게 된 셈이다. 이걸 matplotlib으로 어째저째 잘 표현하면..

'Computer Science > AI(ML, DL, RL, etc)' 카테고리의 다른 글
| ML에서 특성 스케일 맞추기 (0) | 2025.12.26 |
|---|---|
| ML에서 누락된 데이터를 다루기 (0) | 2025.12.25 |
| 원숭이도 알아 먹을 수 있는 VAE 설명 (0) | 2025.07.01 |




