벡터장의 flux, 발산 정리, 그린/스토크스의 정리

벡터장의 flux

?????????

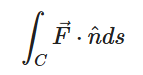
flux의 경우는 간단하게 말해서, 단위 시간당 경로를 따라 빠져나간 유입/유출량이 얼마인가? 를 따진다고 볼 수 있다. divergence의 경우는 미소 영역(점?)에 대해 논하지만, flux의 경우에는 좀 더 스케일이 커진 케이스라고 볼 수 있을 것이다.

이 벡터장은 중심에서 바깥으로 퍼져 나가는 형태이고, 모든 점에서 Divergence가 양수일 것이다. 물론 Flux라고 해서 크게 다를건 없어 보이고, 실제로도 양수이다. 결론적으로 경계 안/밖으로의 유입/유출량에 대한 정보가 Flux가 될 것인데, 근데 왜 공식이 저렇게 되는지 의문이 들 수 있을 것이다.

 

아래와 같은 조건이 있다고 해보자.

• 파란 화살표는, 각 면의 중점에서 측정한 벡터장이다.
• 빨간 화살표는, 각 면의 단위 법선 벡터(Normalized Vector)이다.

이때 각 면에서의 유입/유출량은 (벡터에 단위법선벡터를 내적한 것)이 되고, 이 값이 클수록 벡터가 해당 사각형(선만 있는거!)를 통해서 강하게 빠져나가거나 반대거나 뭐 그럴것이다. 그렇게 하면 전체 Flux는 아래와 같이 근사 되는데,

 

이걸 한계 과정(아주 작은 조각으로 나눈 다음에, 무한히 합치는 것)으로 지지고 볶으면 Divergence로 연결이 되고, 결국에는 위와 같은 수식이 나오게 된다.

 

다만 문제는, flux의 공식 자체는 다변수이므로 하나의 변수로 정리해야 좀 정신 건강이 좋아진다는 점이다. 외부 법선을 직접 구하는 것은 그다지 뇌 건강에 좋지 않다. 따라서 일반적으로는 Normalized Vector를 접선 벡터의 -90도 회전으로 표현하게 되는데, 이에 대한 회전변환행렬은 [[0, 1], [-1, 0]]이 된다. 그러니까 어떤 벡터의 두 변수 컴포넌트를 바꾸고, 새로 들어온 y컴포넌트에 -1을 곱하면 

와 같이 된다. 분모의 값은 "Normalized"이기 때문에 붙은 거다. 이때 피타고라스 정리에 따라서 길이요소는 아래와 같이 정리되고, 이걸 가져다 쓰면 성공적으로 나온다.

Flux가 단위 시간당이라는 것을 잊지 마시라.

 

발산 정리

벡터장이 잘 주어져 있고(P(x,y), Q(x,y)) 선적분의 방향은 면적 A의 경계에 대한 반 시계방향이라고 하면

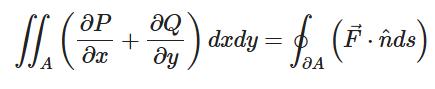
가 성립한다. 무슨 소리냐면, 닫힌 경로에 대해서 유입/유출량은 그 경로로 구성된 면적의 전체 유입/유출량과 같다는 소리다. 왼쪽 식이 Divergence의 총합이라는 사실은, Divergence 공식을 기억한다면 금방 알 수 있을 것이다. 참고로 오른쪽의 적분 기호에 동그라미가 붙어있는데, 저친구는 폐곡선에 대한 선적분을 의미한다.

 

생각을 해보면 당연한 게, 어떤 물통에 들어있는 물의 양이 변했다면 - 그것은 입구를 통해 빠져나간 물의 양과 동일할 것이다. 그리고 발산정리도 크게 다르지 않다. 다만 수식적인 증명을 원한다면, 다른 사이트를 참고하시라.

 

 

 

그린 정리

벡터장이 잘 주어져 있고, 선적분의 방향은 면적 A의 경계에 대한 반 시계방향이라고 하면

가 성립한다. 참고로 우변은 선적분이고, 좌변은 영역 내부의 회전량이 된다. 잠만, 회전량이면 Curl과 연관이 있지 않겠는가? 그리고 발산 정리와 형태가 상당히 유사한데... 그린 정리는 "경로를 따라 흐른 총 순환량 == 영역 내부에서의 전체 회전량"이라는 뜻을 가지기 때문이다.

 

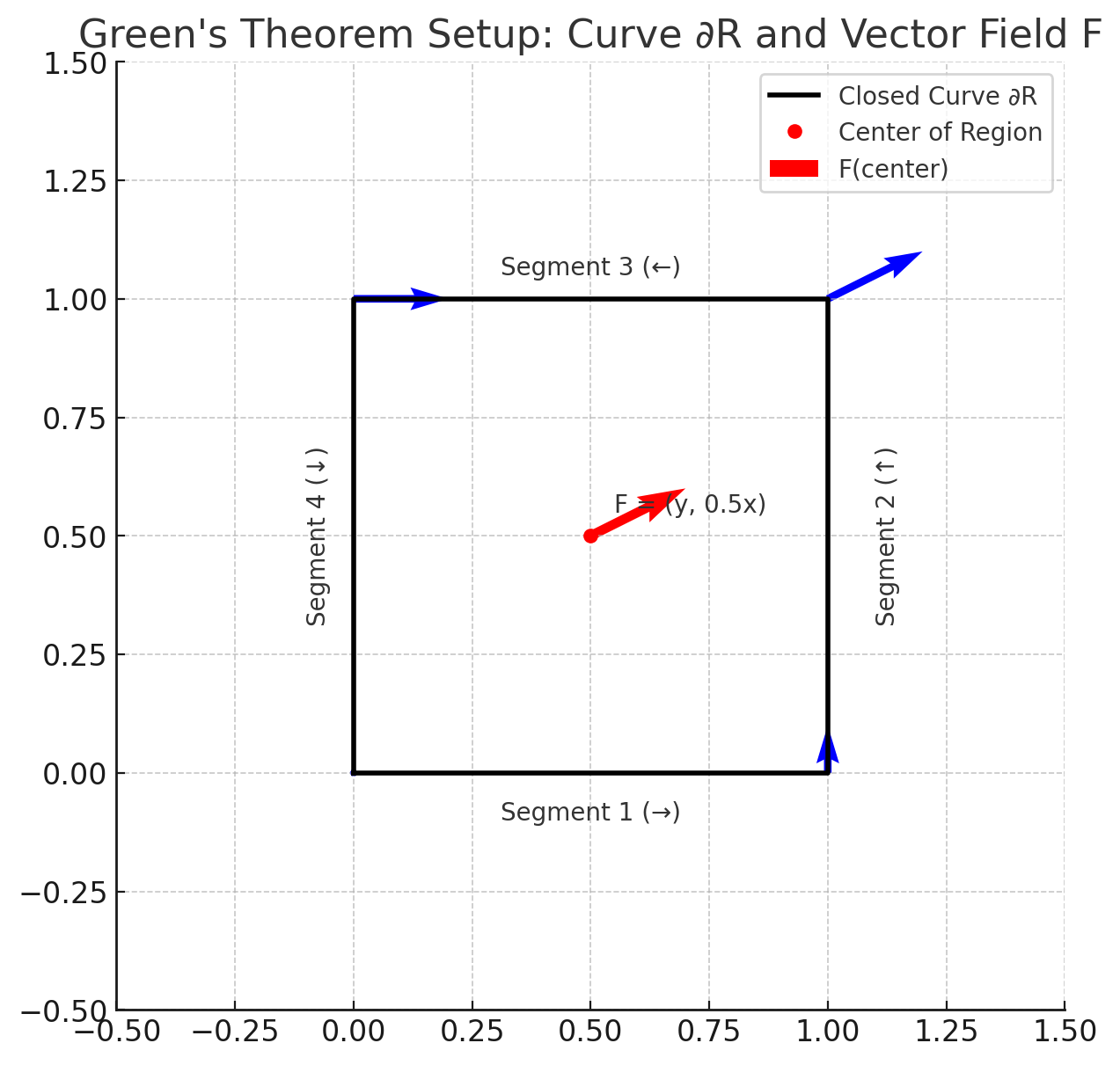
위에서 검은 사각형을 선적분 할 경로, 파란 벡터들을 각 꼭짓점에서의 벡터장, 빨간 점을 사각형 중앙 (면적 적분시 평균 지점), 빨간 벡터를 중심에서의 F라고 해보자. 보면 빨간 벡터와 파란 벡터가 동일하다는 것을 알 수 있다. 참고로 수식적인 증명은 다른 포스트를 참조하시라.

 

 

 

스토크스 정리

그냥 그린 정리의 3차원 버전이다. 먼저 아래와 같은 조건이 있다고 해보자 :

• 회색 면은 적분하려는 곡면 S이다. (단, z=0 평면 위의 사각형이다.)
• 빨간 선은 면의 경계곡선이다.
• 파란 벡터는 각 점에서의 벡터장이다.
• 초록 화살표는 면의 단위 법선 벡터에 대해서, 우변에서 내적할 방향이다.

이럴 경우, 스토크스 정리는 "곡면의 경계를 따라 흐른 순환량이, 그 면 안에서의 회전량 총합과 같다." 고 정리할 수 있다. 회전량이든 유입/유출량이던 결국엔 발산 정리에서 이야기 했던 물통 비유가 성립하게 된다. (물론 유클리드 좌표계에서.)