Divergence, Gradient, Curl, Laplacian

Vector Filed(벡터장)은 유클리드 공간의 각 점에 벡터를 대응시킨것을 의미한다. 반면에 Scala Field라고 하면은, 유클리드 공간의 각 점에다가 어떤 스칼라 값을 대응시킨 것을 의미한다.

 

이때 이들에 대한 연산은 여러가지가 있다. 그중 대표적인 것은 Divergence, Gradient, Curl등이 있는데, 아래에서 소개하도록 하겠다.

Ref : Encyclopedia Magnetica, 가장 잘 설명한 그림인 것 같아서 가져왔다.

 

Divergence (발산, Vector Field -> Scala Field)

Divergence는 발산이라는 뜻을 가지고, 아마도 기초 미적분학에서는 무한급수의 수렴/발산 판정법을 다룰때 들어 봤을 것이다. 물론 Vector Field에 대한 Divergence는 수렴/발산을 말하는 건 아니고, 임의의 한 점이라는 엄청 작은 공간 (자세한건 해석학 전공한 교수님께 물어보는 것이 좋을 것이다.)에서 벡터장이 퍼지는지(위 그림을 보면 이해가 될 것) 아니면 모이는지 정도를 측정하는 것을 의미한다.

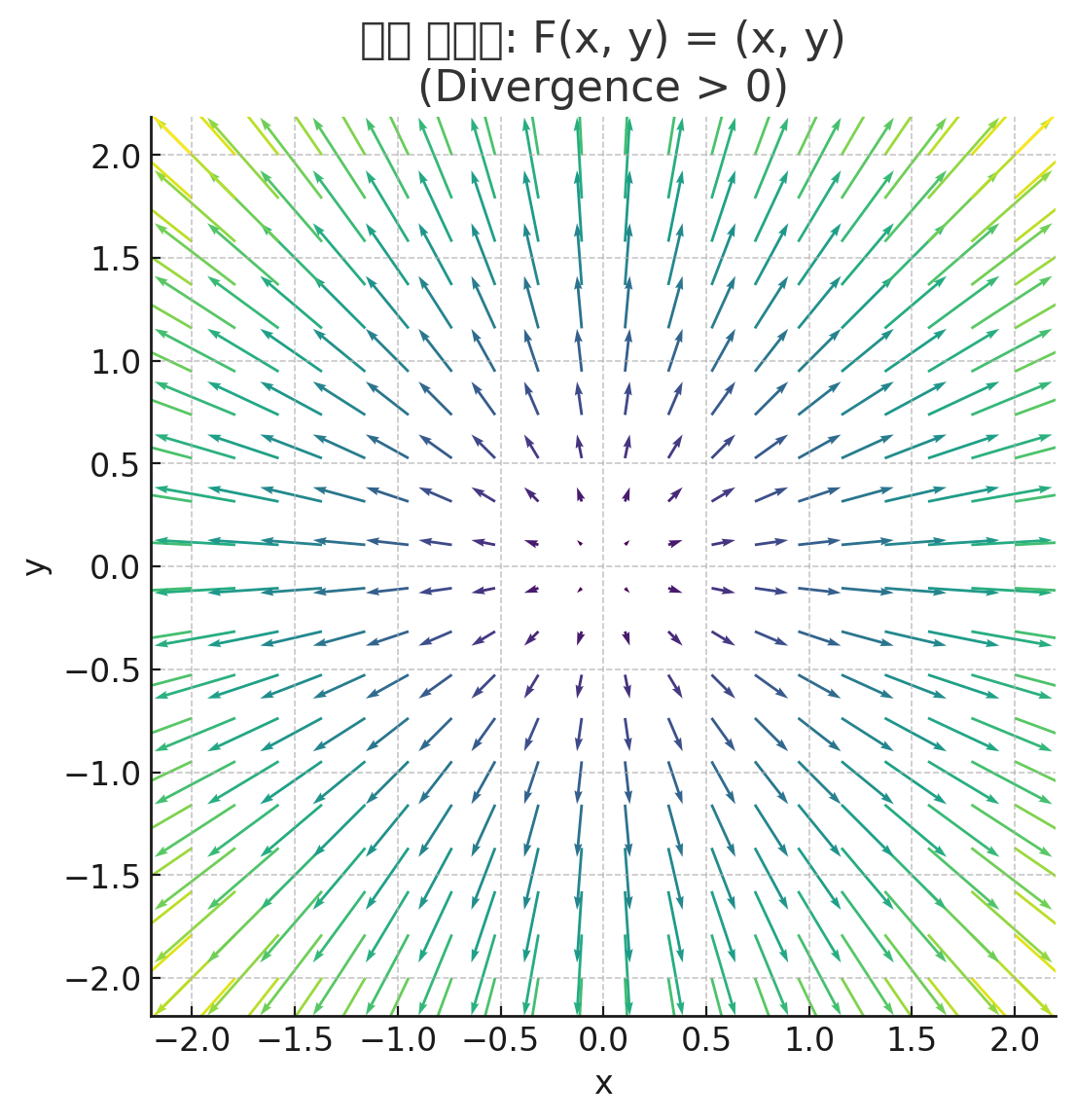
위와 같은 Vector Field가 있다고 해보자. 대충 (0,0)에서 벡터장이 퍼지는 걸 볼 수 있다. 근데 논제는 임의의 점이라는 엄청 작은 공간에서 발산량을 확인해야 한다. 이럴때는 미소 영역에서의 벡터의 발산량을 생각하면 된다. (물론 특정 영역에서 구하면 안되냐고 할 수도 있는데, 평균변화율 보다 순간변화율을 많이 쓴다는 점을 비유로 들어 넘어가자.)

 

엄청 작은 미소영역 dy*dx가 있다고 하면, 여튼 x축 방향으로의 벡터 유입/유출 및 y축 방향으로의 벡터 유입/유출만 생각하면 된다. 영역인데 왜 2축만 다루냐 하면은, "미소영역"이라는데 주목했으면 좋겠다. 어쨋든 벡터의 발산량 자체는 각 축에대한 (유츌량-유입량)의 합이 될것이고, 벡터 함수 f(x,y) = P(x, y)*i + Q(x, y)*j라 하면 미소영역의 발산량은 편미분의 정의 ∂P/ ∂x + ∂Q/ ∂y가 될 것이다. 저게 뭔소린지 모르겠다면, 편미분에 대해서 다시 공부하고 오시라.

여튼 이걸 가지고 벡터함수에다가 지지고 볶아야 하는데, 결론적으로 이야기 하면

Ref : 공돌이의 수학정리노트, 그는 신이다.

가 된다. 델(나블라) 연산자와 벡터 함수를 스칼라곱(내적) 하면 발산량이 나온다.

 

근데 이쯤되면 델(나블라)연산자가 왜 나왔는지 모를 것이다. 그건 밑에서 Gradient를 보시라.

 

 

 

 

Gradient (경사, Scala Field -> Vector Field)

결론적으로, Gradient는 n축 각각에 대한 편미분 값을 원소로 하는 벡터(i, j, k...)를 출력해준다.

말 그대로다.

그리고 위는 ▽f와 같이 표기 가능하며, 이때 ▽을 Del 연산자라고 한다.

 

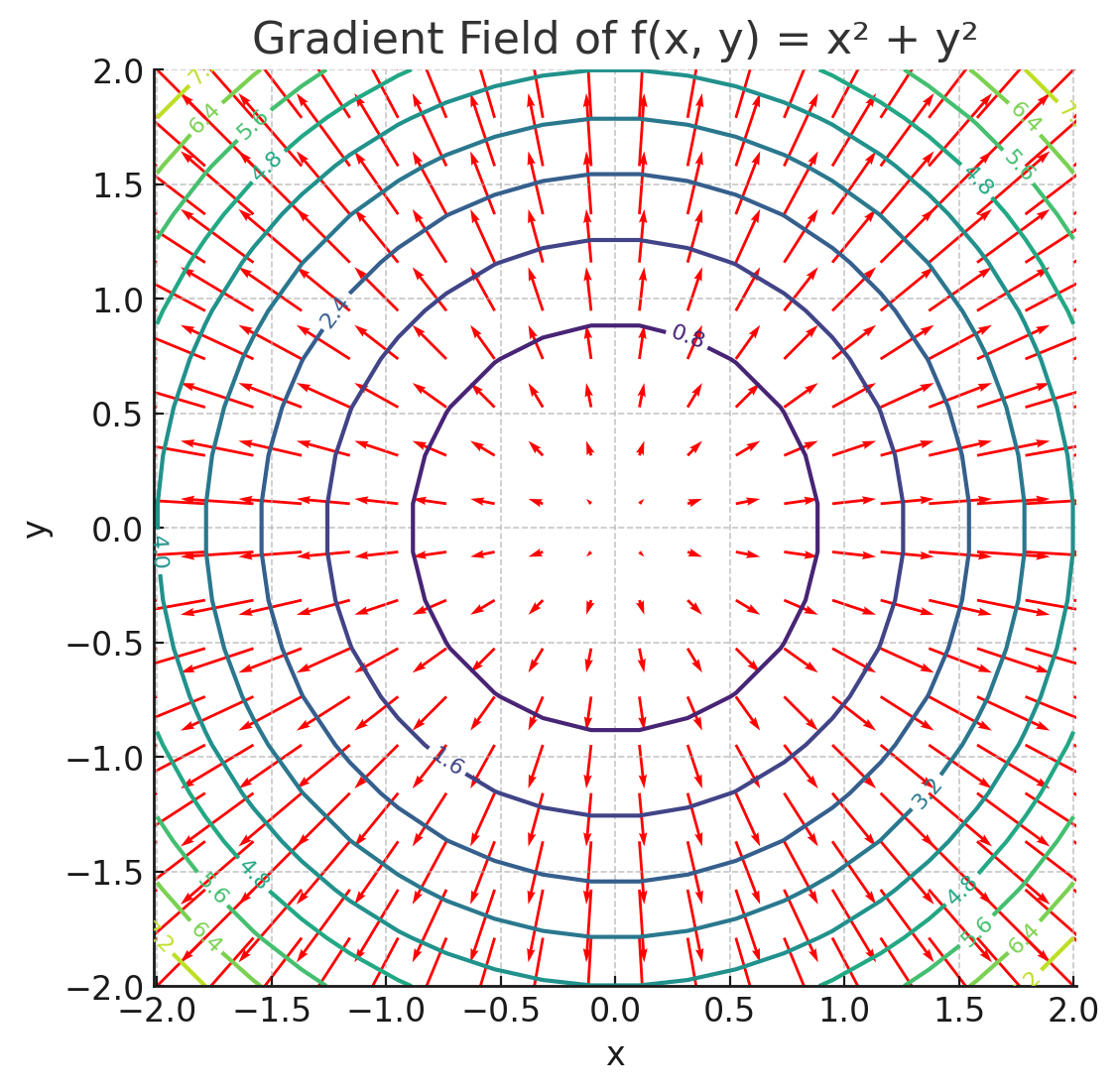
등고선은 f의 높이(값)이고, 빨간 화살표는 gradient 백터이다. 이제 뭔 소리인지 감이 오는가?

참고로 x축 편미분에 대한 벡터와 y축 편미분에 대한 벡터를 더했기에 gradient 벡터들이 저렇게 나오는 것이다. 만약 f(x)의 그래프를 그리게 된다면, f(x)는 밑으로 움푹 파인 싱크홀 마냥 나올 꺼고 gradient 벡터들은 아래에서 위로 향하는 방향이 될 것이다. 이게 일반적인 통념이랑은 좀 다를 수 있는데, Gradient Vector는 "함수값이 가장 빠르게 증가하는 방향"을 가리키기 때문이다. 참고로 ML에서 주구장창 나오는 Gradient Descent는 gradient 방향의 반대로 움직이게 되는 것이다.

 

그리고 이걸 감안해서 Divergence를 생각한다면 - 벡터장이 향하는 방향으로의 변화량을 확인하기에 Divergence는 나블라와 벡터장 f(x,y)를 내적(왜 내적하는지 모르겠다면 기하 교과서의 내적의 도형적 서술을 참조하라.)이라고 볼 수도 있다.

 

 

 

Curl (경사, Vector Field -> Vector Field)

솔직히 Curl은 좀 머리 아프다. 단순하게 설명하자면 미소 면적이 받는 회전력인데, 이를 감안해서 잘 지지고 볶으면 아래와 같은 공식이 하나 나오게 된다. (설명은 머리 아프므로, 다른 문서를 참조하시라.)

이게 잘 이해가 안된다면, 대충 결과값이 물리학 시간에 배웠던 FBI(또는 오른손 법칙)을 연상하면 편하다. 실제로도 그렇게 따라간다.

 

 

Laplacian

유클리드 공간에서 두 번 미분할 수 있는 스칼라 함수 f가 있다 치면, 라플라시안은 f에 대한 그레디언트의 발산이다.

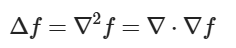
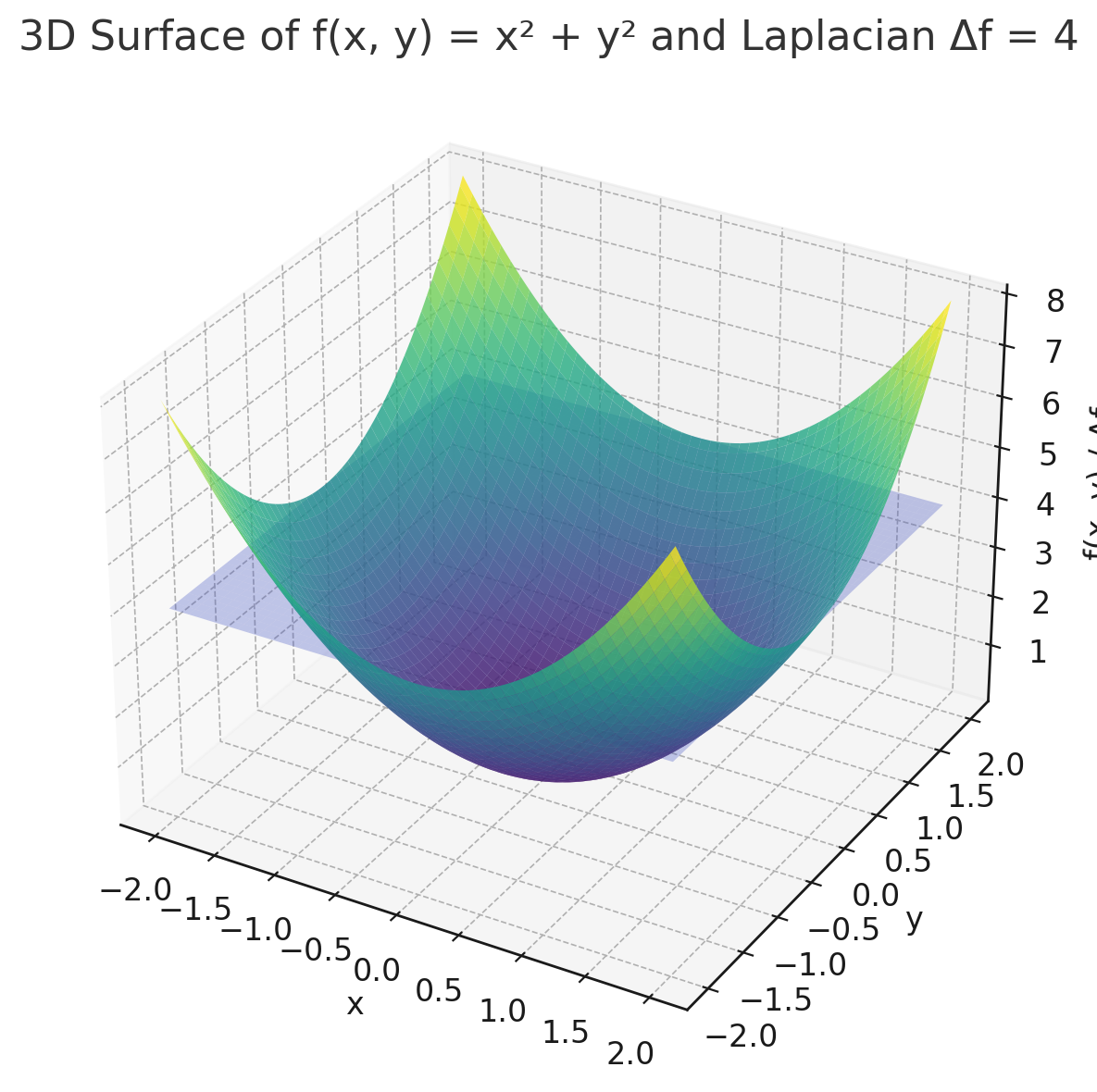
이제 저 밑에다가 Gradient를 그려 보자. 그러면 중심에서 발산하는 모양이 될것이고, 거기에 대한 Divergence를 구하면 양수가 된다. 반대로 저 도형을 뒤집으면, Divergence가 음수가 된다. 이계도 함수가 스멀스멀 생각나지 않는가? 그러니까, Laplacian이 양수면 아래로 볼록한거고, 음수면 위로 볼록한 셈이 되는 것이다.

 

 

 

 

 

 

---

Ref : https://angeloyeo.github.io/2019/08/28/laplacian.html